In this post I will propose a way to solve a sudoku puzzle with a computer program, trying to find all the puzzle solutions in an efficient way using an algorithm based on reduction of Uncertainty.

The basic idea and the source code date from 2005, when the puzzle became popular in Europe.

The algorithm basis

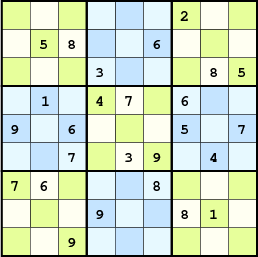
A sudoku puzzle consists of 9×9 squares accepting digits between 1 and 9. A digit placed in a square cannot be repeated in its row, column, or 3×3 grid. Therefore, each square belongs to 3 uniqueness constraint groups (a row, a column and a 3×3 grid), having a total amount of 3×9 constraint groups, 9 of each type.

Each square has a state: a set of digits that can be fit without violating its 3 uniqueness constraints, and therefore the total board state will be the set of all the 81 individual states. Without any information - an empty sudoku - the initial state is the one with the maximum uncertainty: all the digits are possible in each square.

The state of a square gives us a metric of uncertainty, i.e., the number of possible digits. By adding up the uncertainty of each square, we can obtain a global uncertainty metric. Our strategy will be to reduce this uncertainty until we reach the minimum state: the solution.

We have two ways to perform this reduction:

1. Using deductions: given a state, we move to other state with lower uncertainty. The new state will be valid whenever so is the original one. We say a state is valid when it contains the solution, which is actually not easy to determine. Fortunately, we can at least identify those invalid states that do not respect the uniqueness constraints; those, for sure, will not contain the desired solution. Fair enough.

2. Using hypothesis: given a state where no deductions can be made, we make an assumption which takes us to another state with lower uncertainty. We have no guarantee about the validity of our hypothesis, and hence about the validity of our new states, but a wrong decision will result sooner or later in an invalid state, so we will have the chance to rectify.

Using only hypothesis involves a typical brute-force algorithm. But in this approach, the use of deductions will allow us to drastically reduce the space where hypothesis are made: the lower the uncertainty is, the less assumptions we will need. The key point is that every time we reduce the uncertainty of a square, we can trigger recursively new deductions in their related squares (the ones belonging to its constraint groups), resulting in a notable reduction of the overall uncertainty of the problem.

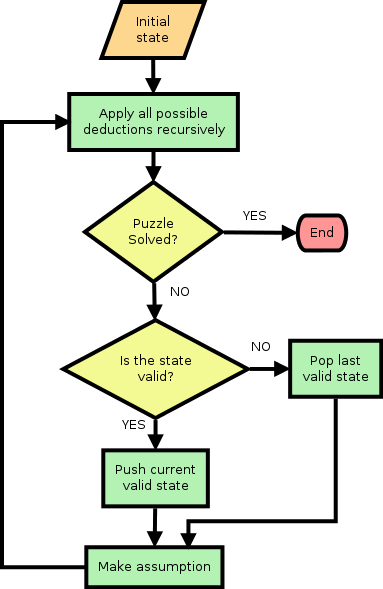
The algorithm will therefore consist of applying deduction rules when possible, and hypothesis when necessary, until we reach the solution. If we reach an invalid state, produced by a hypothesis, we rule out that hypothesis and make a new one. The algorithm flowchart is as follows:

1. We start from the maximum uncertainty state: a void board where all the digits (1..9) are possible in all the squares.

2. Use the initial board information to recursively trigger the initial deductions. If the puzzle is solved, we exit. Many cases can be solved using this technique only.

3. If the puzzle is not solved, we make an assumption over the next square with uncertainty (the next within a given sequence). This will trigger new deductions recursively, with three possible results:

   • If the puzzle is solved, we exit.
   • If we arrive at an inconsistent state, the last hypothesis was incorrect and we try the next possible one over the same square (or, if we cannot make more assumptions over that square, we move to the next one in our sequence).
   • Otherwise - the puzzle is not solved yet - we jump to point 3.

But, how do we exactly make hypothesis and deductions?. Well, making a hypothesis is not a big deal. It could be, say, to randomly pick a digit among the state of a given square (set of possible digits), and suppose it is indeed the correct choice. These are the kind of assumptions we will consider in this program. But we could have chosen other options, like, for instance, assuming that one or more of the possible digits are not possible in the given square. This approach - not explored in this post - could give a better performance, as it could minimize mistakes by choosing more likely options.

Well then, and what about the deductions?. Let’s start with the easy case: if we know that a square contains a given digit, that digit cannot appear in the same row, column or 3×3 grid. That digit can therefore be removed from the state of all the related squares.

Let’s say it in a different way: if a given constraint group has a square whose state contains one single digit (no uncertainty at all), that digit necessarily has to belong exclusively to that square, and the uncertainty of the other squares can be reduced.

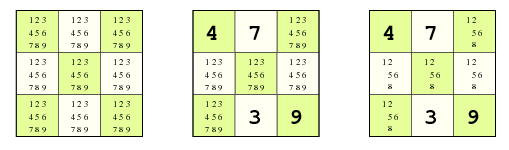
What if we have, in a given constraint group, two squares accepting the same pair of digits and nothing else?, don’t panic: those two digits must be distributed only between those two squares, no other square in the group can accept any of them, and hence their uncertainty can be reduced by removing them from their states.

Can we generalize this rule? certainly. By simple induction, if we want to distribute a set of N digits among the squares of a constraint group, and there are exactly N squares accepting only digits from that set, those N digits necessarily have to be distributed among those N squares, and the other 9 - N squares can’t receive any of them.

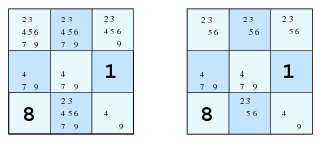
Let’s say it again, in a more formal way this time: given a restriction group C - a set of 9 squares -, let A be the state of one of them - the set of possible digits of that square - and let B be the set of squares of C with their state contained in A. If the cardinal of A is the same as the one of B, then the squares of C which are not contained in B - i.e., C \ B - can’t contain any element of A in their states. Thus, those elements can be removed from their states, and, consequently, the uncertainty is reduced.

That’s all, this is the basic rule, we don’t need anything else, so let’s start programming.

The code

The program is written in C and has been tested under GNU Linux. More details about its usage and board format can be found in the README file.

The source code is quite clear, so I’ll just give some guidelines to help its understanding:

• About the data model, the structures square_t and square_group_t respectively model a square and a restriction group. No more complex data structures are needed.
• Regarding that the square state is coded as a bit field (an unsigned short where the least significant 9 bits represent the possible digits), the following bitwise operations can be done:
  • An uncertainty reduction operation consists in removing a bit subset from a bit set: a &= ~b (the set b is removed from a).
  • A set inclusion can be detected checking the equality: if ((a | b) == b) … (is a contained in b?)
  • The number of considered digits (the number of set bits) can be computed with the GCC built-in function __builtin_popcount.
  • The digit coded by a set of bits with only one set bit can be obtained with the GCC built-in function __builtin_ffs, wich returns the first set bit index.
• The method uncertainty_reduction performs a deduction rule over a square (the recursion enables to trigger other reductions in the related squares), and the method make_assumption makes a hypothesis.

Links

• Sudoku solver hosted on github.com
• Sudoku solver source code