Arithmetic operations with arbitrary precision

I decided to write this small library in 2000, after watching a rerun of “The Simpsons” episode “Treehouse of Horror VI”.

Figure 1: Homer Simpson in a three-dimensional world.

In the last story of this episode, Homer Simpson jumps into a three-dimensional world. The full story, and specially this parallel world, are full of mathematical tributes: geometrical shapes, Euler’s identity, a reference to the P versus NP problem, and so on. Among these mathematical references, a disturbing numerical formula attracted my attention:

$1782^{12} + 1841^{12} = 1922^{12}$

The previous statement is obviously a joke, since it contradicts Fermat’s Last Theorem. However, evaluating both sides of the equation with a scientific calculator, one can fall for it. Try with Google, for example:

The problem with is that a normal calculator doesn’t handle the enough amount of significant figures. Given the fact that both sides of the equality share the 9 first digits, the result is, apparently, the same. Here is the full 40-digit result:

The main trouble stems obviously from a spatial limitation of the display, unable to represent all the computed figures in scientific notation. But even if our device had a larger screen, the above formulas couldn’t be properly evaluated due to the internal floating point storage precision.

Even though there are numerous tools able to perform arithmetic operations with arbitrary big integers (like the phyton language, or GNU bc), I found interesting, as part of my learning process, to write a lightweight and generic library to deal with this and other similar problems.

In this post I will present the library code and its basic structure, and in future publications we will try to improve its efficiency and show some practical examples.

Library specification

The library works with natural binary-coded decimal (NBCD) format, with sign and module agreement, so an arbitrarily big integer can be encoded in a - long enough - BCD digit sequence.

Figure 2: BCD sequence.

In order to handle fractional numbers, the library uses fixed-point arithmetic, therefore the format - the BCD sequence - is divided into integer and fractional parts. This way, fractional numbers can be approximated with arbitrary precision by simply allocating enough memory in the fractional part. This scheme can deal with arbitrary-sized numbers, but in a static way, i.e., having previously allocated the needed memory.

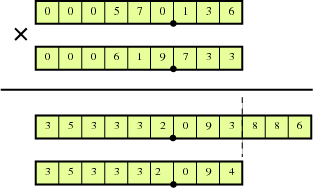
Figure 3: Multiplication with fixed-point arithmetic.

Once the format has been chosen, let us describe some simple arithmetic operations:

Addition and subtraction: These operations are made by a point-wise addition or subtraction of both BCD sequences, applying a carry propagation from each digit to the next one.
Multiplication: The operation is performed by a typical long multiplication algorithm.
Division: The algorithm used is the long division algorithm.

The code

The library is coded in C++, but without exploiting many of the features of the language.

A number is coded in BigNumber class, which consists basically in a byte array and a sign flag. For simplicity and clarity, only one decimal digit is coded in each byte, instead of two per byte.

The file config.h is a configuration point, where we can set the number of digits assigned to the integer and fractional parts in the format.

The file test.cc contains a main function with an example application: it evaluates both sides of the former equation $1782^{12} + 1841^{12} = 1922^{12}$ , and verifies its falseness. At least 40 digits are needed to carry out the operation, so the default configuration, which reserves 50 digits for both the integer and fractional parts, is enough for our purposes.

The rest of the files implement several operations.

addsub.cc: addition and subtraction.
mul.cc: multiplication.
div.cc: division.
convert.cc: conversion between bignumbers and floating point numbers.

Ibán Cereijo

Arithmetic operations with arbitrary precision

Library specification

The code

Links