A fast circle algorithm for ZX Spectrum

My first steps in computer programming were with an old ZX Spectrum, like many other people of my generation. Following a natural order, Sinclair BASIC was the first language I dealt with, but quite often the hardware limitations forced me to move to the Z80 assembly language. A common practice was to code some “time critical” routines - like some graphic routines - in assembly to avoid many of the bottlenecks.

In this post, I’ll explain, as an example, how to outperform the built-in circle drawing routine.

Algorithm explanation

The original built-in algorithm (command CIRCLE in BASIC) drew the circumference with an angular sweep, from 0 to 360 degrees, and although it was probably implemented in assembly, it seemed rather slow.

It is possible to outperform the original implementation without using trigonometric functions nor square roots, and even without using multiplications. The following algorithm is equivalent to the now known mid-point algorithm, but with different error formulation, and it is based on the implicit equation of the circumference. Such equation is, assuming the circle centered at (0,0):

$x^2 + y^2 - r^2 = 0$

To draw the contour, we establish $(x,y) = (r,0)$ as the starting point, and draw the first octant, with angles between 0 and 45 degrees. Below 45 degrees the $y$ component goes faster than the $x$ one, so we will increment the $y$ coordinate inside a loop, and correct the path decreasing the $x$ component whenever we consider we are “far away” from the contour. To evaluate how far we are, let’s compute the squared error

$e(x,y) = x^2 + y^2 - r^2$

Figure 1: Sweep from 0 to 45º and pixel discretization.

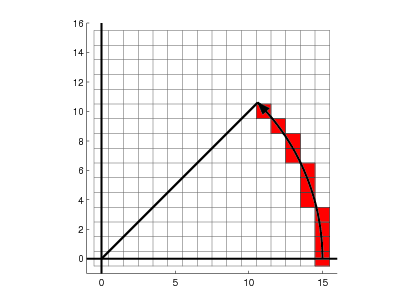
Let $\vec{p}_{k} = (x_{k},y_{k})$ be the coordinates of a pixel at a given step k; at each step we have to choose whether to move upwards or towards the upper-left pixel:

$\begin{array}{l} \vec{p}_{1,k+1} = \vec{p}_{1,k} + (0,1)\\ \vec{p}_{2,k+1} = \vec{p}_{2,k} + (-1,1) \end{array}$

Our decision will be based on a minimum squared error criterion; for the two options above we have the following expressions for the error (in our discrete space, we measure at the middle of the pixels, so the mathematical center is at the middle of the pixel (0,0))

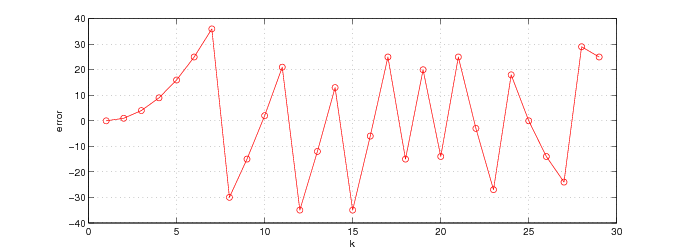
$\begin{array}{ll} e_{1,k+1} = & e(\vec{p}_{1,k+1}) = x_{k}^2 + (y_{k}+1)^2 - r^2 = e_{k} + 1 + 2\,y_{k}\\ \\ e_{2,k+1} = & e(\vec{p}_{2,k+1}) = (x_{k}-1)^2 + (y_{k}+1)^2 - r^2\\ &= e_{1,k+1} + 1 - 2\,x_{k} = e_{k} + 1 + 2\,y_{k} + 1 - 2\,x_{k} \end{array}$

Notice that we can know the error at a given step if we know the error previous to it, with only a few additions. Whenever $|e_{1,k+1}| < |e_{2,k+1}|$ , we choose $\vec{p}_{1,k+1}$ as the next pixel, otherwise we take $\vec{p}_{2,k+1}$ . We can simplify the comparison in the following way, knowing that $e_{2,k+1}$ is always negative and $x_{k}$ and $y_{k}$ are integers

$\begin{array}{l} |e_{1,k+1}| < |e_{2,k+1}| \,\,\,\, \Rightarrow \,\,\,\, e_{1,k+1} < -e_{2,k+1} \,\,\,\, \Rightarrow \,\,\,\, e_{1,k+1} < -e_{1,k+1} - 1 + 2\,x_{k} \\ \,\,\,\, \Rightarrow \,\,\,\, 2\,e_{1,k+1} < 2\,x_{k} - 1 \,\,\,\, \Rightarrow \,\,\,\, e_{1,k+1} < x_{k} - \frac{1}{2} \,\,\,\, \Rightarrow \,\,\,\, e_{1,k+1} < x_{k} \end{array}$

The initial value for the error is $e_{0} = 0$ , because the first pixel $\vec{p}_{0} = (r,0)$ satisfies the circle equation. Observe the evolution of the error in the figure below; the corrections produced by the decrements in the $x$ component help to keep the error around $0$ .

Figure 2: Evolution of error in the angular sweep from 0 to 45º. While incrementing the y component, we correct the x component whenever the error becomes too high, according to a minimum squared error criterion. Each x correction results in an error reduction.

The algorithm can be coded in C as follows:

int x = r;
int y = 0;
int e = 0;

for (;;) {
  drawPixel(xc + x, yc + y);
  if (x <= y) {
    break;
  }
  e += 2*y + 1;
  y++;
  if (e > x) {
    e += 1 - 2*x;
    x--;
  }
}

Once we know how to draw the first octant, the rest of the circle can be drawn applying symmetry. Instead of drawing one single pixel, we draw 8 of them:

Figure 3: Simmetry.

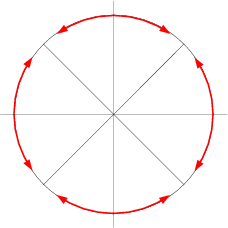
drawPixel(xc + x, yc + y);
drawPixel(xc + x, yc - y);
drawPixel(xc - x, yc - y);
drawPixel(xc - x, yc + y);
drawPixel(xc + y, yc + x);
drawPixel(xc + y, yc - x);
drawPixel(xc - y, yc - x);
drawPixel(xc - y, yc + x);

The code

The source code is a .asm text file that you can compile with a z80 assembler like pasmo (you can use other assemblers, but some of them ignore the ORG directives, so be careful with the relocations). With pasmo you can generate directly a .tap file ready to be loaded in an spectrum emulator.

The code contains two main functions: one for drawing pixels and another one for drawing circles. Also, the file includes an execution example placed at the address 53000, that draws a set of concentric circles growing in size.

For drawing pixels, two lookup tables are used: tabpow2, with powers of 2, and tablinidx, with the order of the 192 screen lines (remember that the ZX spectrum used an interlaced access).

You can invoke the routine by placing the point coordinates at the addresses 50998 and 50999, and jumping to the address 51000

POKE 50998, 128
POKE 50999, 88
RANDOMIZE USR 51000

To invoke the circle routine, you must place the center coordinates at 51997 and 51998, and the radius at 51999, and then jump to the address 52000.

POKE 51997, 128
POKE 51998, 88
POKE 51999, 80
RANDOMIZE USR 52000

In this video you can see the execution of the following code under Spectemu emulator, comparing the performance of the two algorithms.

10 FOR i=1 TO 20
20 CIRCLE 128, 80, i
30 NEXT i
40 RANDOMIZE USR 53000

Ibán Cereijo

A fast circle algorithm for ZX Spectrum

Algorithm explanation

The code

Links